이 수치는 영점으로 부터 얼마나 떨어져있느냐..


타고 들어 가면 더블로 되어있다~
▶ 벡터란?
ㆍ 벡터는 크기와 방향을 정의하는 값. 일반적으로 화살표로 그려져 화살표의 길이가 벡터의 크기를 나타내고
화살표의 방향이 벡터의 방향을 나타낸다, 좌표계에서 예시를 보는게 아래 그림

ㆍ 벡터는 물리학에서 속도, 가속도 등과 같은 개념을 표현하는데 주로 사용하지만....
ㆍ 그래픽스 프로그래밍에서는 위치,이동,회전 등 다양한 개념을 표현하는데 사용
예를들어 3D공간에서 점A에서 점B로 이동하는 것은 벡터로 표현할 수 있다.

▶ 3차원 공간에서의 벡터
ㆍ 3차원 공간에서 벡터는 보통 (x,y,z)형태의 순서쌍으로 표현되며 각 성분은 x축, y축, z축에 대한 방향성을 나타냄
예를들어 (1,0,0)은 x축 방향으로 크기 1인 벡터를 의미한다

▶ 벡터의 표현

▶ 영백터와 기저벡터 ( 단위벡터 )

ㆍ 모든 성분의 값이 0인 벡터를 영벡터
ㆍ 축을 기준으로 각각 성분의 값이 1이며 크기가 1인 벡터를 표준기저벡터 또는 단위벡터 라고 한다.
▶ 벡터의 덧셈과 뺄셈
ㆍ 벡터의 덧셈과 뺄셈은 각 성분별로 수행됩니다. 예를들어 두 벡터 A = (Ax,Ay,Az)와 B= (Bx,By,Bz)가 있다면
→ A + B = (Ax + Bx, Ay + By, Az - Bz)
→ A - B = (Ax - Bx, Ay - By, Az - Bz)

⊙ 언리얼엔진에서 지원하는 덧셈뺄셈 함수


▶ 벡터의 곱셈
ㆍ 스칼라 곱
ㄴ> 벡터를 스칼라(실수)로 곱하는 것은 각 성분을 그 스칼라 값으로 곱합니다. 예를들어 벡터A와 스칼라s가 있다면
→ s * A = (s * Ax, s * Ay, s * Az)

⊙ 언리얼엔진에서 지원하는 곱셈 함수


▶ 벡터의 내적 ( Dot Product )
⊙ 구하는 식
ㆍ 내적은 두 벡터의 방향성을 비교하는데 사용됩니다. 내적의 결과는 스칼라입니다. 두 벡터 A와 B가 있다면
→ A ㆍ B = AxBx + AyBy + Az*Bz

ㆍ 성분 별 곱셈 후 그 결과를 모두 더한 것입니다. 나오는 값은 스칼라값이며 내적은 두 벡터 사이의 각도를 계산하는데 사용됩니다.
ㆍ 만약 A와 B가 모두 단위 벡터(모두 1인 벡터)라면 A*B = cos(θ)이 됩니다, 여기서 θ는 A와B사이의 각도입니다.
⊙ 기하학적 의미
ㆍ 투영

ㆍ 두 벡터가 이루는 각도에 따라서 위와 같이 부호가 결정됩니다.
ㆍ 물체의 위치를 나타내는 벡터와 특정 평면의 법선벡터(평면에 수직인벡터) 간의 내적을 계산하면 그 결과는 물체가 평면의 어느쪽에 있는지를 알려줍니다. 내적이 양수라면 물체는 평면의 한쪽에 있고 음수라면 반대쪽에 있습니다.
ㆍ 내적에 스칼라 곱셈
ㆍ 일반적으로 벡터의 방향은 유지하면서 그 크기를 조절할 필요가 있을 때 스칼라 곱셈이 사용됩니다.

ㆍ 투영되는 벡터가 단위벡터가 아니라면 내적된 결과에 길이를 곱해주면 된다. (단위벡터일시 0)
ㆍ a와 b 벡터가 있고 k가 스칼라값일때 " k * b "는 벡터 b의 각 성분을 k 배 확대한 새로운 벡터를 생성합니다.
그리고 이렇게 만들어진 새로운 벡터와 a의 내적을 구하는 것이"a ⋅ (kb)"입니다.
ㆍ 결과는 원래 두 백터 a,b의 내적에 k를 곱한 값과 동일하므로 분배법칙이 성립합니다 "k * (a * b) "
ㆍ 교환법칙 또한 성립합니다.
ㆍ 두 벡터 사이의 각도가 주어졌을때, 한 벡터의 길이를 확장하고 싶으면 해당 벡터에 cos(θ)를 곱해주면 됩니다.
ㆍ 벡터의 길이 계산

ㆍ sqrt(v,v)
ㆍ cos(θ)?
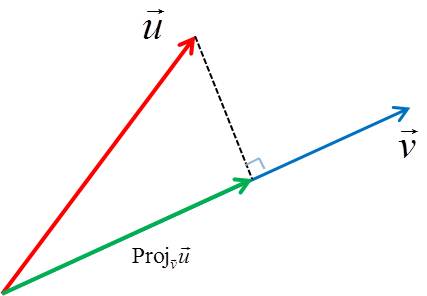
ㆍ v벡터가 단위벡터라고 했을때 투영된 벡터의 길이가 내적이다.
ㆍ 위 그림을 보면 u벡터를 빗변 투영된 벡터를 밑변으로 하는 직각삼각형으로 볼 수있다.
ㆍ u벡터의 길이가 1이라면 내적값을 직각삼각형의 성질을 통해 코사인값으로 표현할 수 있다.

a ㆍ b = ||a||*||b||*cos(θ)
ㆍ acos함수를 통해 두 벡터의 성분값만 할면 두 벡터가 어떤 각도로 배치되어 있는지도 알 수 있다.
θ = acos(a*b)
⊙ 언리얼엔진에서의 사용 예시
ㆍ 언리얼 엔진에서는 예를들어 캐릭터가 특정 방향을 바라보고 있는지 판단할 때 내적을 사용할 수 있습니다.
캐릭터의 전방향 벡터와 목표지점을 가리키는 벡터 사이의 내적 값을 확인함으로써 캐릭터가 목표지점을 바라보고 있는지 확인 여부를 알 수 있습니다. 또한 AI가 플레이어가 시야 안에 있는지를 확인하거나 조명, 그림자 효과를 구현하거나 다양한 상황에서 활용됩니다.
⊙ 언리얼엔진에서 지원하는 내적구하는 함수


▶ 벡터의 외적 (Cross Porduct)
ㆍ 외적은 주로 두 벡터에 수직인 새로운 벡터를 찾는데 사용됩니다. 만약 두 벡터A와 B가 있다면
→ A X B = ((Ay,Bz) - (AzBy), (AzBx) - (AxBz), (AxBy) - (AyBx))
ㆍ 외적은 주로 두 벡터가 형성하는 평면에 수직인 방향을 찾거나, 두 벡터가 이루는 면적을 구하는데 사용됩니다.
ㆍ 식의 결과 벡터는 원래의 두 벡터에 수직이며 그 크기는 원래의 두 벡터가 이루는 평행사변형의 넓이와 같습니다.


ㆍ 언리얼 엔진에서는 예를들어 비행기가 특정 축 주위로 회전하려 할 때 외적을 사용해여 해당 축을 구할 수 있습니다.
⊙ 언리얼엔진에서 지원하는 외적구하는 함수

